今回はディープニューラルネットワークから始まります。
ディープニューラルネットワーク
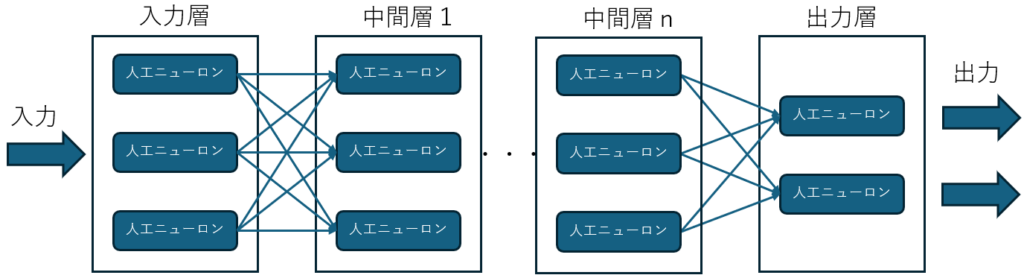
この絵の様に、ニューラルネットワークの中間層が多段になっているものがディープニューラルネットワークです。
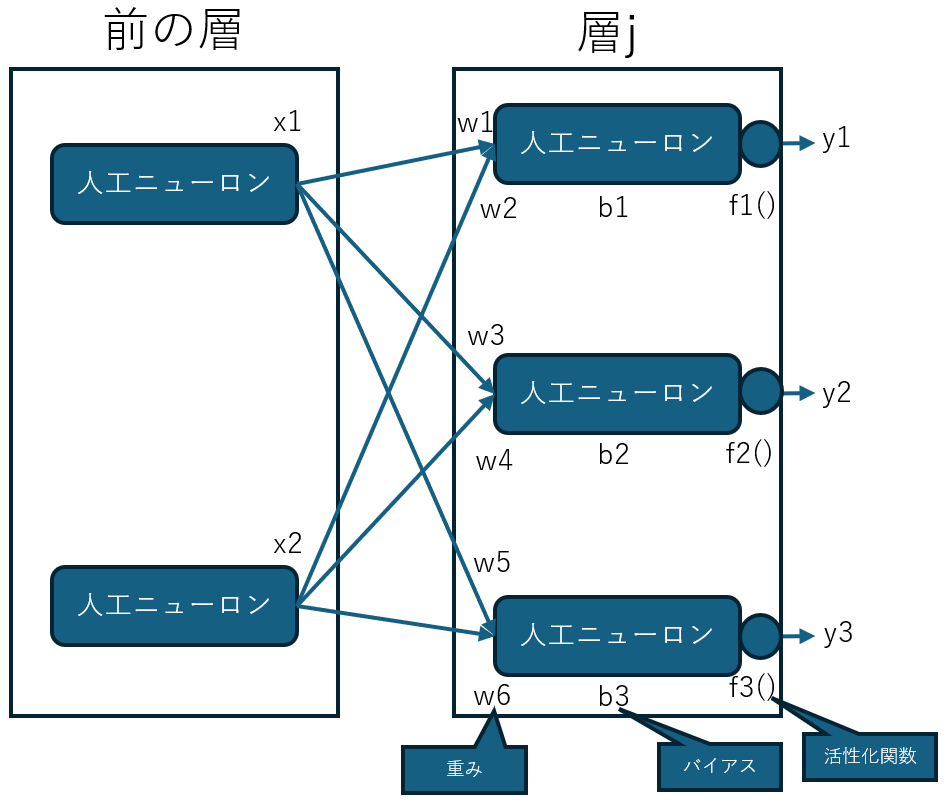
演算は行列積で行われます。
前の層のニューロンが2つ、後の層のニューロンが3つの場合、xは前の層の出力、wは重み、bはバイアスとして
y1=f1(w1・x1+w2・x2+b1)
y2=f2(w3・x1+w4・x2+b2)
y3=f3(w5・x1+w6・x2+b1)
層jのニューロンはそれぞれ前の層の出力を全て受け取って、それに重みを掛けたものにバイアスを加え、これを活性化関数を通して次の層への入力とします。
活性化関数
活性化関数には問題の種類によって適・不敵が有ります。二値分類ならシグモイド関数、中間層で良く使われるのはレル関数、出力層では回帰問題なら恒等関数や、分類問題ならソフトマックス関数など。
例えば、恒等関数は入力をそのまま出力します(y=x)、レル関数はxが0以下ならy=0、xが正数ならy=x、など。
活性化関数が無ければ、層(計算)をいくら重ねても最終的には1つの式で表現できてしまい直線的な関係しか表現出来ませんが、活性化関数を導入する事で曲線的な関係を表現することができ表現力が上がります。
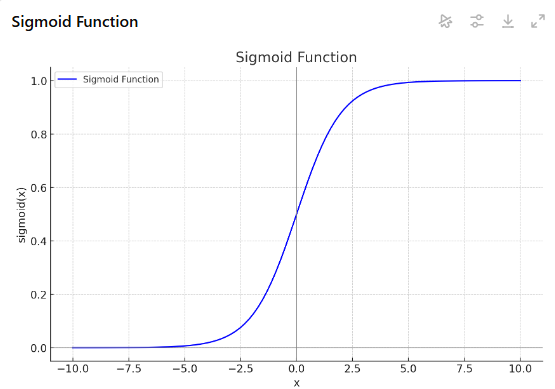
これはシグモイド関数です
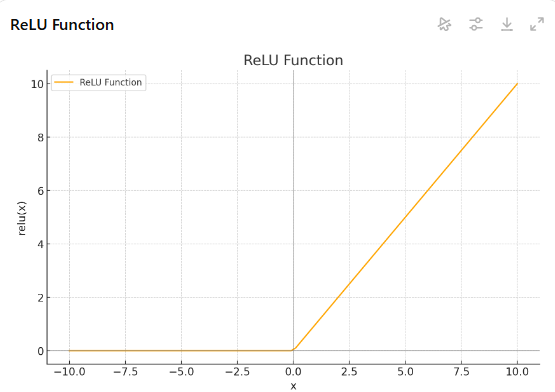
これはReLU関数です
バイアス
バイアスが何故必要なのか?については難しい説明が有りそうですが、単純に入力が0の時でも何らかの出力を得られる様にするため、と理解しています。
次は学習に入っていきますが、ちょっとずつ進みましょう。
2024年11月5日 手塚幹人
コメント